Représenter l’argent de plusieurs façons : additions, fractions et équivalents

Aidez vos élèves de 3^e année du primaire à utiliser la monnaie, à comprendre les fractions et à représenter l’argent de différentes manières. Faites une seule des activités ou faites-les toutes dans l’ordre indiqué dans la leçon.

Vue d’ensemble

Concept

Nous nous servons de différentes combinaisons de billets de banque et de pièces de monnaie pour représenter la même valeur. L’argent est une façon courante d’utiliser les fractions dans la vie de tous les jours.

Durée

105 minutes pour la leçon et les exercices mathématiques

Niveau scolaire

3^e année du primaire

Domaines d’apprentissage

Mathématiques

• Calculer la monnaie nécessaire pour les paiements en argent d’un dollar et de montants de moins d’un dollar
• Trouver différentes façons de représenter le même montant d’argent
• Simuler différents coûts et déterminer les pièces de monnaie et les billets de banque nécessaires pour payer
• Représenter et résoudre des problèmes de partage en parts égales en utilisant l’argent et les fractions équivalentes

Objectifs d’apprentissage

Les élèves seront appelés à :

• utiliser diverses stratégies pour déterminer la valeur de différentes combinaisons de pièces de monnaie ou de billets de banque;
• représenter un montant d’argent à l’aide de différentes combinaisons de pièces et de billets;
• déterminer le montant nécessaire pour payer à partir de problèmes écrits et numériques;
• reconnaître les différentes coupures de billets de banque et pièces de monnaie utilisées au Canada.

Matériel

Fournitures scolaires et technologies nécessaires

• crayons
• imprimante
• tableau blanc et marqueurs (ou tableau interactif ou projecteur)
• pièces de monnaie canadiennes de jeu ou réelles (facultatif)
• deux dés (facultatif)

Feuilles de travail

1. Téléchargez les feuilles d’activité et de réponse.
2. Imprimez les feuilles de travail et les graphiques pertinents pour chacun des élèves :
   • 1^re activité : Calculer la monnaie 1 et Calculer la monnaie 2
   • 2^e activité : Même montant, différentes formes et Combien de monnaie?
   • 3^e activité : Partage équitable : les fractions et Partager avec ceux qu’on aime

1^re activité : Rendre la monnaie lors de transactions simples

Durant cette activité, les élèves calculent le montant d’argent nécessaire pour des opérations simples et la monnaie rendue quand on paie avec une pièce de monnaie ou un billet de banque de valeur supérieure. La première activité fait appel à des montants en dollars et la deuxième, à des montants de moins d’un dollar.

Remettez à chaque élève les feuilles de travail « Calculer la monnaie 1» et « Calculer la monnaie 2».

Durée

30 minutes

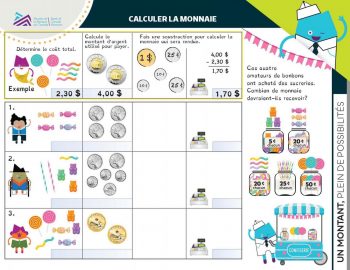
1.1 Activité de la feuille de travail : Clients distraits

Commencez par la première page. Pour chaque question, les élèves doivent indiquer l’élément qui manque : le montant du paiement, la monnaie rendue ou la valeur de l’achat.

Répondez à la première question en groupe, puis demandez aux élèves de travailler individuellement ou en petits groupes pour les exemples suivants. Remarquez que la difficulté des questions augmente quand les montants augmentent.

Quand les élèves auront terminé la feuille de travail, utilisez la clé de réponse pour faire la correction en groupe.

Passez en revue la dernière question (5) en groupe. Vérifiez si les élèves ont répondu « 5 $ ». Demandez‑leur pourquoi la personne a décidé de payer avec 22 $ alors que le prix était inférieur à 20 $.

Expliquez aux élèves que les gens paient parfois avec plus d’argent que nécessaire pour recevoir un billet en retour plutôt que de la petite monnaie. Si vous avez le temps, vous pouvez vous exercer en groupe au moyen des exemples suivants :

• Si quelque chose coûte 6 $ et que vous voulez qu’on vous rende un billet de 5 $, combien d’argent devez-vous donner? (11 $)
• Si quelque chose coûte 14 $ et que vous voulez qu’on vous rende un billet de 10 $, combien d’argent devez-vous donner? (24 $)

Expliquez aux élèves comment ça fonctionne : si vous voulez recevoir un certain montant quand on vous rend la monnaie, ajoutez-le au prix pour déterminer combien d’argent vous devez donner.   

Vos élèves peuvent s’exercer à faire des transactions en dollars entiers dans la première partie de Calculer la monnaie, et des transactions plus complexes dans la seconde.

1.2 Activité de la feuille de travail : Calculer la monnaie

Avant de commencer la feuille de travail, montrez aux élèves des modèles qui leur permettent de compter par bonds pour additionner rapidement. Voici quelques exemples :

• Les bonbons emballés coûtent 20 cents chacun. Les élèves peuvent donc compter par bonds les quatre bonbons à la question 1 de la feuille de travail (20, 40, 60, 80).
• Ils peuvent aussi compter par bonds les pièces de monnaie, comme les quatre pièces de 25 cents à la question 2 (25, 50, 75, 100).

Pour la prochaine activité, expliquez aux élèves qu’ils feront appel aux mêmes compétences mathématiques pour rendre la monnaie en cents lors de l’achat d’articles qui coûtent moins d’un dollar. Demandez-leur d’additionner et d’inscrire dans la première colonne le prix total des bonbons que chacun veut acheter. La deuxième colonne indique le montant d’argent que chacun paie. Dans la troisième colonne, les élèves calculent la monnaie à rendre, inscrivent ce montant et dessinent les pièces de monnaie correspondantes (petits cercles indiquant 5 ¢, 10 ¢, 25 ¢, etc.)

Pour faciliter les calculs, utilisez les approches suivantes :

• Avant d’additionner, écrivez le prix de chaque bonbon à côté du bonbon dans la première partie de la question.
• Comptez par bonds pour trouver le prix de plusieurs bonbons du même type (comme les trois serpents à la question 3), puis additionnez le prix des différents bonbons.

Quand les élèves auront fini, faites la correction en groupe.

2^e activité : Présenter les relations entre les fractions et l’argent

Dans cette activité, les élèves utilisent la monnaie pour comprendre les relations qui existent entre l’argent et les fractions. Ils trouvent aussi des séquences leur permettant de compter plus facilement des montants élevés.

Durée

40 minutes

2.1 Discussion : Séquences

Discutez avec vos élèves des séquences qu’ils ont remarquées dans l’argent.

Posez-leur les questions suivantes pour évaluer leurs connaissances. Comptez par bonds ou faites des multiplications et des divisions pour les aider s’ils ne sont pas sûrs des réponses.

• Il y a combien de pièces de 25 cents dans un dollar? Et combien de pièces de 10 cents? Et de pièces de 5 cents?
• Si vous avez reçu 100 $ en billets de 20 $, combien de billets avez-vous? Et si vous avez reçu 100 $ en billets de 10 $?

Distribuez (ou affichez) le graphique « Même montant, différentes formes ». Dites aux élèves que ce diagramme explique de quelle manière la valeur d’un dollar (ou de 100 cents) peut être exprimée à l’aide de différentes pièces de monnaie. Les pièces correspondent à différentes fractions d’un dollar.

Servez-vous de l’illustration Même montant, différentes formes pour montrer la relation entre les fractions et l’argent.

Montrez aux élèves les différents cercles (pièces de 5, 10 et 25 cents) et la façon dont on peut indiquer les fractions d’un dollar, c’est-à-dire les montants qui le constituent.

2.2 Diagramme d’introduction : Même montant, différentes formes

Présentez ensuite la notion de fraction parallèle avec des montants en pièces de monnaie à l’aide du graphique circulaire qui se trouve à côté du diagramme. Montrez une moitié, un quart ou un cinquième du graphique circulaire en en masquant une partie avec la main ou un morceau de papier. Vous pourriez aussi laminer la feuille et utiliser des marqueurs ou encore projeter le graphique circulaire à l’aide d’un tableau interactif ou d’un projecteur.

Tandis que vous masquez différentes parties du cercle, demandez aux élèves de vous aider à inscrire les réponses suivantes sur le tableau blanc pour chaque fraction que vous examinez :

• la fraction sous sa forme la plus simple (½, ¼ ou ⅕)
• la fraction équivalente avec 100 comme dénominateur (50/100, 25/100, 20/100)
• le nombre de cents nécessaires pour chaque fraction d’un dollar (50 cents, 25 cents, 20 cents)
• l’équivalent décimal de chaque fraction (facultatif) (0,50; 0,25; 0,20)

Montrez la relation qui existe entre la fraction simple et la fraction équivalente en expliquant que ce sont deux façons d’exprimer la même chose. Par exemple, si vous avez un dollar et que quelqu’un en prend la moitié, ce montant de 50 cents est égal à ½ ou 50/100, que cela soit exprimé sous la forme d’une fraction simple ou par rapport à 100 cents (un dollar). Plutôt que de dire qu’on a « un quart de dollar », on dit qu’on a 25 cents.

Vous pouvez mentionner le nom anglais de certaines pièces de monnaie canadiennes, parce qu’il correspond à la valeur de la pièce par rapport au dollar. En anglais, la pièce de 25 cents s’appelle quarter, c’est-à-dire « quart », ce qui est logique. La pièce de 10 cents s’appelle dime, mot qui vient du vieux français disme et du latin decima et qui signifie un dixième. La pièce de 5 cents s’appelait à l’origine half-dime, soit la moitié d’un dime. Les pièces de 50 cents, aussi appelées « demi-dollar », ne sont pas en circulation au Canada et sont rarement utilisées, mais elles existent encore au Canada et aux États-Unis. La plupart sont des pièces de collection.

Si vous avez le temps, vous pouvez aussi faire l’une des activités suivantes pour aider vos élèves à compter la monnaie afin de se préparer à la prochaine feuille de travail :

• Utilisez des pièces de monnaie de jeu pour représenter et compter différents montants et fractions. Les élèves peuvent placer les pièces directement sur le diagramme pour représenter la fraction (partie d’un dollar). Les pièces de jeu peuvent aussi servir à compter par bonds. Cette feuille de travail contient aussi des activités permettant de compter par bonds.
• Avec toute la classe ou en petits groupes, demandez à chacun de vos élèves de dire tout haut un montant indiqué sur le diagramme et le nom d’une pièce de monnaie contenue dans le cercle (par exemple, « 65 cents en pièces de 5 cents »). Les élèves devront ensuite essayer d’être les premiers à dire le nombre exact de pièces nécessaires pour obtenir ce montant.

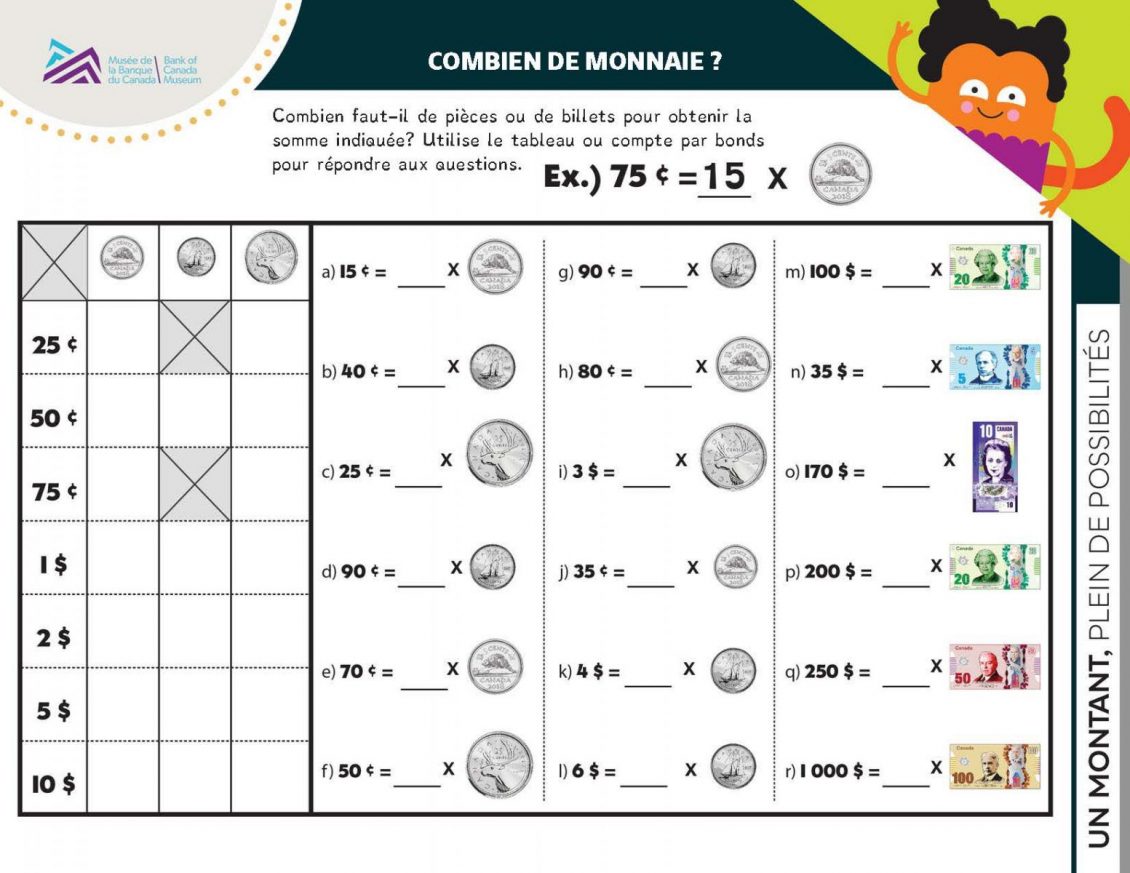
2.3 Activité de la feuille de travail : Combien de monnaie?

Distribuez la feuille de travail « Combien de monnaie? ». Discutez en groupe de la première rangée du tableau de la tâche 1, à titre d’exemple (pour avoir 25 cents, on peut réunir 5 pièces de 5 cents ou une pièce de 25 cents).

Selon leurs besoins, demandez aux élèves de continuer à répondre aux questions du tableau, seuls ou en équipes de deux. Ils peuvent consulter le diagramme en cercles de la feuille de travail précédente, au besoin. S’ils ont besoin d’aide, montrez-leur les éléments ci-dessous :

• Pour trouver le nombre de pièces de 5, 10 et 25 cents nécessaires pour avoir 2 $, on peut doubler chaque montant de la rangée précédente (pièces nécessaires pour avoir 1 $).
• On peut calculer le nombre de pièces de chaque type qui est nécessaire pour avoir 5 $ en additionnant deux fois le nombre de la rangée correspondant à 2 $, puis en y ajoutant le nombre de la rangée correspondant à 1 $.
• Pour constituer les nombres de la rangée correspondant à 10 $, on peut doubler les nombres nécessaires pour la rangée correspondant à 5 $.
• On ne peut pas avoir 75 cents à partir de pièces de 10 cents seulement. Expliquez qu’en additionnant des pièces de 10 cents (comme quand on compte des dizaines), on peut seulement obtenir un nombre qui finit par 0. Si vous avez déjà parlé des décimales, vous pouvez utiliser cet exemple pour montrer la réponse sous la forme d’un nombre décimal (7,5).

Faites la correction en groupe.

Utilisez Combien de monnaie? pour aider vos élèves à trouver des séquences ou constantes permettant de compter la monnaie.

3^e activité : Diviser de l’argent en utilisant les fractions

Dans cette activité, les élèves devront confirmer l’argent dont ils ont besoin pour acheter certains articles et ils le représenteront en utilisant différentes combinaisons de pièces de monnaie.

Durée

30 minutes

3.1 Discussion : Diviser de l’argent en parts égales

Avant de leur remettre la feuille de travail, demandez aux élèves s’ils ont déjà vu des gens partager (diviser) de l’argent en deux ou trois parts égales. Comment feraient-ils pour diviser de l’argent entre deux personnes? Comment feraient-ils pour un billet de 20 dollars, par exemple? Et s’ils devaient partager cinq dollars?

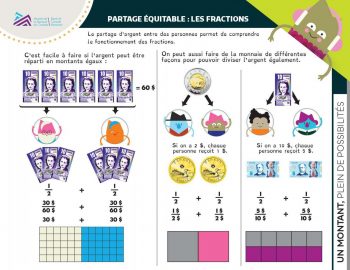
Il est possible que les élèves donnent des exemples correspondant à ceux qui figurent à la première page de la feuille de travail « Partage équitable : les fractions ». Trouver des équivalents d’argent (ou des plus petits montants) est une bonne introduction à l’activité.

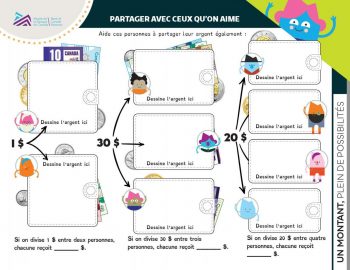
3.2 Activité de la feuille de travail : Partage équitable : les fractions et Partager avec ceux qu’on aime

Distribuez les feuilles de travail. Suivez les étapes décrivant la façon de partager de l’argent de façon égale entre plusieurs personnes. Montrez aux élèves que lorsqu’on divise de l’argent, on fait une fraction. Le montant total (ou 1/1) équivaut à deux montants égaux plus petits quand il est partagé en deux. Les fractions montrent une partie du tout; quand on partage un montant en deux, la fraction est 1/2. (Expliquez aux élèves que le nombre total de parties est indiqué dans le bas de la fraction, qui s’appelle le dénominateur. Le nombre du haut est le numérateur, qui indique le nombre de parties du tout.)

Dites-leur qu’on peut utiliser les fractions pour montrer comment on divise – ou on partage – l’argent. Étant donné qu’on ne peut pas partager un billet de banque entre deux personnes, on peut échanger le billet contre de plus petits billets qui représentent, ensemble, un montant équivalent. On peut ensuite diviser ces billets de valeur inférieure, au besoin. Présentez l’exemple en utilisant des pièces de monnaie pour diviser une pièce de 2 dollars.

Aidez les élèves à comprendre pourquoi certains montants sont faciles à diviser. Posez-leur, par exemple, les questions suivantes :

• Est-ce qu’on peut diviser 6 $ en deux parts égales? (Oui, chaque personne reçoit 3 $.) Et 4 $? (Oui, chaque personne reçoit 2 $.)
• De combien de pièces de 2 $ a-t-on besoin pour diviser un montant en parts égales entre trois personnes? (Il faut un multiple de 3, c’est-à-dire 3, 6, 9 ou 12 pièces de 2 $.)
• Aux élèves plus avancés, demandez s’ils remarquent des constantes dans la façon dont on peut diviser des montants en parts égales. Le montant d’argent doit être un multiple du nombre de personnes : par exemple, on peut partager 9 $ en trois parce que 9 est un multiple de 3 (tout comme 3 et 6). De cette façon, les trois personnes obtiennent 3 $ chacune.

Demandez aux élèves de répondre aux trois questions de la page suivante. Montrez-leur qu’ils peuvent utiliser l’espace situé à côté de l’argent pour dessiner le montant d’une façon différente si cela facilite le partage de l’argent. Ensuite, passez les questions en revue en groupe.  

Partage équitable : les fractions est un document explicatif pour apprendre à diviser des sommes d’argent. Il s’accompagne de la feuille d’exercice Partager avec ceux qu’on aime.

3.2.1 Pour aller plus loin

Si vous avez le temps, demandez à vos élèves de s’exercer à partager de l’argent de façon concrète :

• Montrez-leur qu’on divise régulièrement des montants quand on joue à des jeux. Demandez‑leur de se regrouper en équipes de deux ou plus. Donnez à chaque équipe un petit montant d’argent de jeu et désignez un élève qui devra distribuer (diviser) l’argent en parts égales entre les membres de l’équipe.
• Pour une activité plus avancée, demandez aux élèves de lancer deux dés afin de générer des problèmes mathématiques liés à l’argent. Le chiffre d’un dé détermine un montant d’argent en coupures de 10 $ (depuis 1, qui correspond à 10 $, jusqu’à 6, qui correspond à 60 $). L’autre dé détermine combien de personnes doivent se répartir ce montant (de 1 à 6). Étant donné que toutes les combinaisons de montant et de personnes ne peuvent pas être résolues à l’aide d’une division simple, encouragez les élèves à lancer de nouveau les dés au besoin. Notez que toute combinaison difficile que vous aimeriez résoudre plus tard (p. ex., 30 $ à répartir entre 4 personnes) demandera l’utilisation de billets de banque et de pièces de monnaie.

Conclusion

Durée

5 minutes

Passez en revue avec les élèves ce qu’ils ont appris sur la façon d’exprimer le même montant d’argent au moyen de différentes combinaisons de billets de banque et de pièces de monnaie. Par exemple, demandez-leur s’ils se souviennent du nombre de pièces de 5, 10 ou 25 cents qu’il y a dans un dollar. Rappelez-leur la relation qui existe entre les fractions et l’argent.

Comme devoir, vous pouvez demander aux élèves qu’ils s’exercent à diviser des montants d’argent avec un adulte, en utilisant des pièces de monnaie ou des billets de banque. Ou bien dites-leur que la prochaine fois où ils seront dans un magasin, ils devront payer en argent comptant avec le montant le plus exact et estimer la monnaie qui leur sera rendue.

Principaux points à retenir

• Différentes combinaisons de billets de banque et de pièces de monnaie peuvent correspondre au même montant d’argent.
• Simuler des achats simples peut être utile pour apprendre à faire des transactions en argent au quotidien.
• Partager – ou diviser – un montant est une façon de représenter l’argent sous forme de fractions.

Activités supplémentaires

Organisez un jeu de rôles permettant aux élèves de s’exercer à payer et à rendre la monnaie. Si vous avez besoin de fournitures, sachez que notre activité Le marché des avatars comprend des modèles de personnages et d’accessoires en papier avec lesquels les élèves pourront organiser leur propre marché.

Utilisez notre foire aux questions sur l’argent et la monnaie pour animer une discussion en classe ou donner des informations générales sur la monnaie canadienne et ses origines.

Retournez aux fractions portant sur l’argent et au graphique de l’équivalent d’un dollar quand vous présenterez le sujet des fractions plus complexes, comme les huitièmes.

Présentez la notion de l’estimation des taxes et du coût d’un achat quand on y ajoute les taxes.